Geldscheintester

Download

Der Java-Quellcode ist für Interessierte verfügbar. Leider habe ich nix kommentiert, bei ca. 130 Zeilen sollte das auch nicht weiter problematisch sein.

Der Euro kommt !

Natürlich wird auch die neue Währung ein Sicherungssystem verwenden. Ob dies wieder eine Variante der Dieder-Gruppen ist, kann ich nicht sagen, da ich noch keinerlei Informationen über die Euro-Geldscheine besitze.

Literaturhinweis

Eine sehr interessante Quelle war die Computerzeitung

c't 04/1997, S. 448.
Die erste Anregung kam aus der Vorlesung Diskrete Strukturen von Prof. Budach in meinem ersten Studiensemester.

navigator: home

programming

Geldscheintester

Der Geldscheintester

Gleich zu Beginn sollte hier nach wenigen Sekunden ein Java-Applet erscheinen. Falls es das nicht tut, so ist entweder

Java nicht installiert (eher unwahrscheinlich) oder aus Sicherheitsgründen deaktiviert.

Einige unsaubere Java-Implementierungen (insbesondere von Netscape) erzeugen Fehler beim Laden des Applets, weil sie nicht vorhandene JavaBean-Konfigurationen abfragen. Ich arbeite daran, das Problem zu lösen.

Ansonsten hier einfach die Seriennummer eingeben, mein letzter Hunni hat z.B. GG6909287Z5 (man beachte, dass die ersten beiden Symbole Buchstaben sind, ebenso das vorletzte), Groß-/Kleinschreibung spielt keine Rolle:

Mit einem ordentlichen Zeichenprogramm, einem guten Drucker nebst Baumwollpapier, Geduld und viel krimineller Energie läßt sich heutzutage Papiergeld auch im Wohnzimmer fälschen. Von allzu offensichtlichen Kopien abgesehen, gibt es nicht wenige, die sich die Mühe machen, "fortlaufende" Seriennummern zu implementieren.

Diese haben jedoch eine eingebaute Sicherung: die letzte Ziffer ist eine Prüfziffer, anhand deren sich die Gültigkeit der 10 vorangegangenen bestimmen läßt. Dass dies recht zuverlässig funktioniert, erkennt man sofort, wenn man nach Belieben einige Zahlen bzw. Buchstaben verändert. Die zur Bestimmung der Prüfziffer verwendete Methodik gewährt Einblicke in die Diskrete Mathematik mit ihren Permutationen und Dieder-Gruppen.

Prüfziffern

Der Ursprung der Prüfziffern liegt in der Kontrolle von Zifferncodes, die Verfälschungen unterliegen können. Denkbare Störquellen sind menschliche Tippfehler, wie z.B. Zahlendreher, aber auch Signalrauschen, das zu optischen oder akustischen Mißinterpretation führt.

Sehr einfache Verfahren beruhen auf modulo-10-Operationen. Häufig benutzt wird der Rest der Division der 10 der Quersumme des Zahlencodes. Somit fallen Einzelfehler (z.B. "5" statt "6") auf, Zahlendreher werden aber nicht entdeckt. Bessere modulo-10-Verfahren schaffen auch das, aber mathematisch ist es erwiesen, daß sie nie alle Einzelfehler und Zahlendreher erkennen können.

Die ISBN-Nummern von Büchern werden auch durch eine modulo-prüfziffer abgesichert, hier kommt aber eine spezielle modulo-11-Technik zum Zuge, die alle Einzelfehler und Zahlendreher zuverlässig erkennen kann. Nur ist damit auch ein elftes Symbol notwendig und der Ziffernvorrat reicht damit nicht mehr aus. Die Zuhilfenahme des "X" behebt dieses Problem, doch nicht immer kann man solche Lösungen implementieren. Der andere mögliche Weg, alle Zahlencodes, die das elfte Symbol als Prüfziffer hätten, auszuschließen, war indiskutabel, da dies 10% des Zahlenraumes vernichten würde. Bei 12 verwendeten Ziffern, wären 1,2 "überflüssig", also wären dann auch 2-stellige Prüfziffern überlegenswert.

Dieder-Gruppen

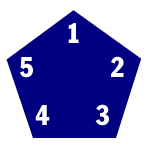Neben der modulo-10-Addition gibt es noch eine weitere Gruppe, die auf den 10 Ziffern operiert: die Diedergruppe D₅ (sprich:"Di-eder"). Diedergruppen entstehen aus geometrischen Transformationen, die n-Ecke auf sich selbst abbilden. Die D₅-Gruppe bezieht sich somit auf 5-Ecke, die durch 5 Rotationen und 5 Spiegelungen insgesamt 10 Abbildungen ergeben. Es werden den Rotationen die Ziffern 0 bis 4 und den Spiegelungen 5 bis 9 zugeordnet. Somit ist 0 das Einselement, das inverse Element ist für 0<n<5 das Element 5-n und für n>4 ist es n.

Das interessante an dieser Gruppe ist, dass sie nicht kommutativ (also nicht abelsch) ist. Ein Beispiel hierfür ist: 1*6=7 aber 6*1=5. Diese Eigenschaft ist gerade für die Erkennung von Zahlendrehern enorm wichtig.

Auf Geldscheinen findet man genau diese Technik wieder. Hierbei wird die Prüfziffer derart gewählt, dass die Dieder-Verknüpfung aller Stellen stets 0 ergibt. Die Buchstaben dienen ebenfalls der Absicherung gegen Fehler, besonders der letzte verhindert Dreher der letzten beiden Positionen. Dies ist unbedingt notwendig, da es, obwohl D₅ nicht abelsch ist, ein paar Elemente gibt, für die doch wieder a*b=b*a gilt. Zum Überlick hier die Bedeutungen der Buchstaben:

A	D	G	K	L	N	S	U	Y	Z
0	1	2	3	4	5	6	7	8	9

Die Verknüpfungstabelle sieht folgendermaßen aus:

*	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9
1	1	2	3	4	0	6	7	8	9	5
2	2	3	4	0	1	7	8	9	5	6
3	3	4	0	1	2	8	9	5	6	7
4	4	0	1	2	3	9	5	6	7	8
5	5	9	8	7	6	0	4	3	2	1
6	6	5	9	8	7	1	0	4	3	2
7	7	6	5	9	8	2	1	0	4	3
8	8	7	6	5	9	3	2	1	0	4
9	9	8	7	6	5	4	3	2	1	0

Wie bereits erwähnt, gilt für einige Elemente das Kommutativgesetz. Um aber Zahlendreher zu unterbinden, werden die einzelnen Ziffern (bzw. die zugeordneten Buchstaben) permutiert, d.h. vertauscht. Eine Permutation, die dies leistet, ist p = {1, 5, 7, 6, 2, 8, 3, 0, 9, 4} (in der Bedeutung, dass p(1)=1, p(2)=5, p(3)=7 usw.). Sie ist gleichzeitig in der Lage, phonetische Fehler, wie 14 statt 40, zu erkennen. Es gibt noch diverse andere Permutationen, die das gleiche leisten, sie werden meist durch Probieren gefunden.

Die Permutationen lauten dann:

p₁ =	{1, 5, 7, 6, 2, 8, 3, 0, 9, 4}
p₂ = p(p₁) =	{5, 8, 0, 3, 7, 9, 6, 1, 4, 2}
p₃ = p(p₂) =	{8, 9, 1, 6, 0, 4, 3, 5, 2, 7}
p₄ = p(p₃) =	{9, 4, 5, 3, 1, 2, 6, 8, 7, 0}
p₅ = p(p₄) =	{4, 2, 8, 6, 5, 7, 3, 9, 0, 1}
p₆ = p(p₅) =	{2, 7, 9, 3, 8, 0, 6, 4, 1, 5}
p₇ = p(p₆) =	{7, 0, 4, 6, 9, 1, 3, 2, 5, 8}
p₈ = p(p₇) =	{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
p₉ = p(p₈) =	{1, 5, 7, 6, 2, 8, 3, 0, 9, 4}
p₁₀ = p(p₉) =	{5, 8, 0, 3, 7, 9, 6, 1, 4, 2}
p₁₁ =	{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

Es ist unschwer zu erkennen, dass aufgrund der besonderen Struktur von p₈ auch p₉ = p₁ gilt usw. Eine kleine Variation hat sich die Deutsche Bundesbank noch bei der letzten Stelle der Seriennummer einfallen lassen, sie wird nicht permutiert.

Mit diesem Wissen ist es jetzt möglich, die Seriennummer eines deutschen Geldscheines auf seine Gültigkeit hin zu überprüfen. Nimmt man den eingangs erwähnten Hunderter, so bedeutet seine Seriennummer
GG6909287Z5 nach Ersetzung der Buchstaben
22690928795 und Permutation aller Stellen
70304548025
Nun verknüpfe ich die Ziffern miteinander, beginnend von links:
7*0*3*0*4*5*4*8*0*2*5=0 da 7*0=7, 7*3=9, 9*0=9, 9*4=5, 5*5=0, 0*4=4, 4*8=7, 7*0=7, 7*2=5, 5*5=0.

Weil die Verknüpfung 0 ergeben hat, ist die Seriennummer gültig und der Geldscheinschein entweder echt oder eine richtig gute Fälschung. Doch bevor ich mir darüber zu sehr den Kopf zerbreche, fahre ich lieber schnell zu Mediamarkt und kaufe ich mir mit dem Hunderter ein paar neue Musik-CDs.